Počítání úroků z hlavy

Zkoušeli jste přemýšlet nad tím, za jak dlouho budou Vaše prostředky zdvojnásobeny na účtu, kde se úročí 1 % ročně? Za jak dlouho budou prostředky zdvojnásobeny, pokud investujete do akcií, kde předpokládáte zhodnocení 7 % ročně? Jakému úroku odpovídá situace, kdy se cena Vaší nemovitosti ztrojnásobila během 15 let? Vše je samozřejmě možno počítat přesným výpočtem, ale když sedíte u piva a nechce se Vám to počítat na mobilu a chcete zazářit, jak to zvládnete z hlavy, tak se mohou hodit všemožná aproximační pravidla.

Pravidlo 69

Toto pravidlo Vám pomůže k výpočtu toho, za jak dlouho se Vaše prostředky zdvojnásobí při dané úrokové míře. Například pokud chcete vědět, za jak dlouho se ze 100 000 Kč stane 200 000 Kč, pokud je úročeno 2 % ročně, tak stačí dosadit do pravidla

$T=\frac{69}{I}+0.35,$

kde za I dosadíte hodnotu 2 (tj. výši úrokové míry vynásobené 100). V našem případě platí

$T=\frac{69}{2}+0.35=34.5+0.35=34.85.$

Tato hodnota je přibližná, ale poměrně přesná. Pokud použijeme vzorec pro složené úročení (vysvětlení v našem článku: Úročení na běžném a spořícím účtu), tak získáme z

$200 000 = 100 000\cdot (1+i)^t$

pro i=0.02 po pár úpravách tvar

$t=\frac{\ln(2)}{\ln(1.02)} \doteq 35.003.$

Přesným výpočtem jsme se dostali k výsledku, který je velice podobný tomu přibližnému, jestli se peníze zdvojnásobí za 34.85 let, nebo 35 let již není tak důležité, základní představu už máme.

Co když dosadíme vyšší hodnotu? Bude to stále fungovat? Bude, a stále velice přesně, zkusíme např. 20 % ročně:

$T=\frac{69}{20}+0.35=3.45+0.35=3.8.$

Přesným výpočtem bychom obdrželi

$t=\frac{\ln(2)}{\ln(1.2)} \doteq 3.802.$

To je téměř přesně! Důvod je ten, že pravidlo 69 pracuje nejpřesněji v oblasti kolem úrokové míry 20 % ročně, kdy zaznamenává nejmenší absolutní i relativní chybu (shoda nastává pro úrokovou míru 21.473 %).

Pravidlo 72

Pravidlo má stejný účel jako předchozí, tj. odhadnout, za jak dlouho se prostředky zdvojnásobí. Pravidlo je ještě jednodušší, ale stojí nás to trochu přesnosti. Zde dosazujeme do předpisu

$T=\frac{72}{I}.$

Zkusíme dosadit za I hodnotu 2 a 20 (ať můžeme srovnávat s předchozím) a získáme

$T=\frac{72}{2}=36$

a pro druhý případ

$T=\frac{72}{20}=3.6.$

Vidíme, že rozdíl trochu narostl, ale opět je pravidlo dostačující pro hrubý odhad.

Výhodou pravidla je, že se dá jednoduše upravit pro odhad úrokové míry, která je potřebná pro zdvojnásobení prostředků za zadanou dobu – stačí vyjádřit I, tj.

$I=\frac{72}{T}.$

Ono to je možné i s předchozím pravidlem, ale tam už vyjádření není vhodné k počítání z hlavy. Vraťme se ale k pravidlu 72 a ukážeme si využití pro úrokovou míru. Dejme tomu, že naše nemovitost během 8 let zdvojnásobila hodnotu. Chceme si to srovnat s úrokem v bance a ptáme se na to, jak by musel být vysoký, aby zajistil takto vysoké zhodnocení. Pokud použijeme pravidlo 72, tak získáme

$I=\frac{72}{8}=9.$

Tedy v bance by byla potřeba přibližně úroková míra ve výši 9 % ročně. Ověříme to ještě přesným výpočtem se složeným úročením (vysvětlení v našem minulém článku: Úročení na běžném a spořícím účtu)

$2\cdot P=P\cdot(1+i)^8,$

kde P je původní cena nemovitosti (je vidět, že ji nemusíme znát, hned se nám vykrátí a na levé straně zůstane 2). Získáme

$2=(1+i)^8.$

Teď stačí odmocnit a upravit a máme finální tvar a výsledek

$i=\sqrt[8]{2}-1 \doteq 0.0905,$

tedy úroková míra 9.05 % ročně. Opět je vidět velice dobrá přesnost.

Pravidlo 110 a pravidlo 114

Tato pravidla slouží k tomu, aby se určilo, za jak dlouho se prostředky ztrojnásobí. Pravidlo 110 je, podobně jako 69, trochu komplikovanější a pravidlo 114 je zase obdobou pravidla 72. Obecně pravidla vypadají takto:

$T=\frac{110}{I}+0.52,$

$T=\frac{114}{I}.$

Ukážeme je na příkladu, kdy úroková míra činí 5 % ročně. Přesným výpočtem bychom došli k době 22.52 let. Pokud dosadíme do pravidel, získáme

$T=\frac{110}{5}+0.52=22.52,$

$T=\frac{114}{5}=22.8.$

Opět vidíme dobrou přesnost a stejně jako u pravidel pro zdvojnásobení vkladu můžeme druhé pravidlo použít k odhadu úrokové míry při zadaném čase (lépe se s ním počítá). Pokud budeme mít nemovitost, která během 12 let ztrojnásobila hodnotu a opět si to chceme srovnat s úrokem v bance, tak získáme

$I=\frac{114}{T}=\frac{114}{12}=9.5.$

Tedy v bance by byla potřeba přibližně úroková míra ve výši 9.5 % ročně. Ověříme to ještě přesným výpočtem se složeným úročením (vysvětlení v našem minulém článku: Úročení na běžném a spořícím účtu)

$3\cdot P = P \cdot (1+i)^{12},$

kde P je původní cena nemovitosti. Získáme

$3 = (1+i)^{12}.$

Teď stačí odmocnit a upravit a máme finální tvar a výsledek

$i=\sqrt[12]{3}-1 \doteq 0.0959,$

tedy úroková míra 9.59 % ročně. Opět je vidět velice dobrá přesnost.

Porovnání pravidel

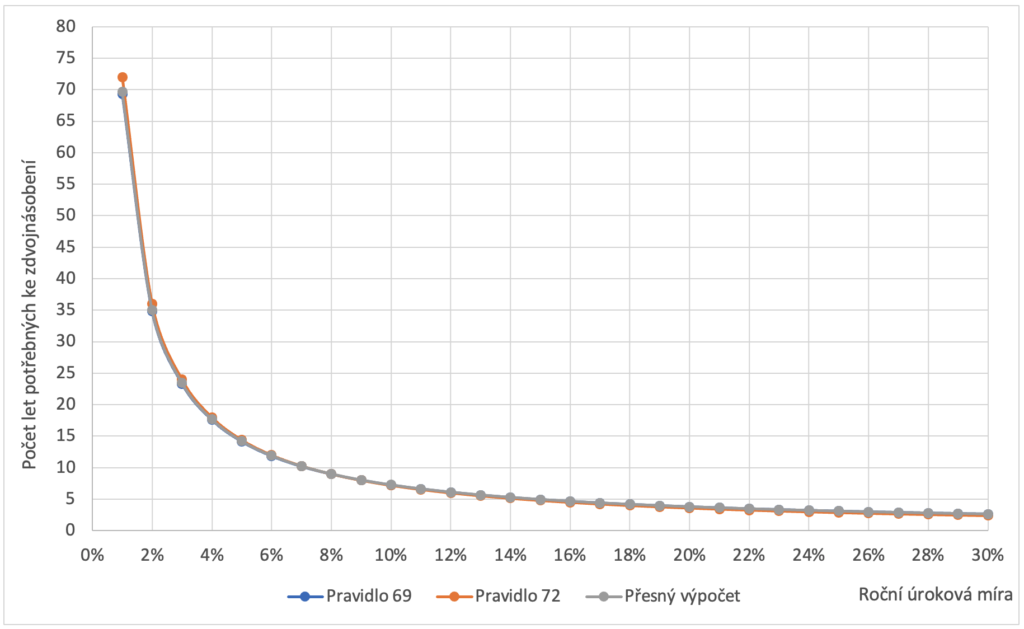
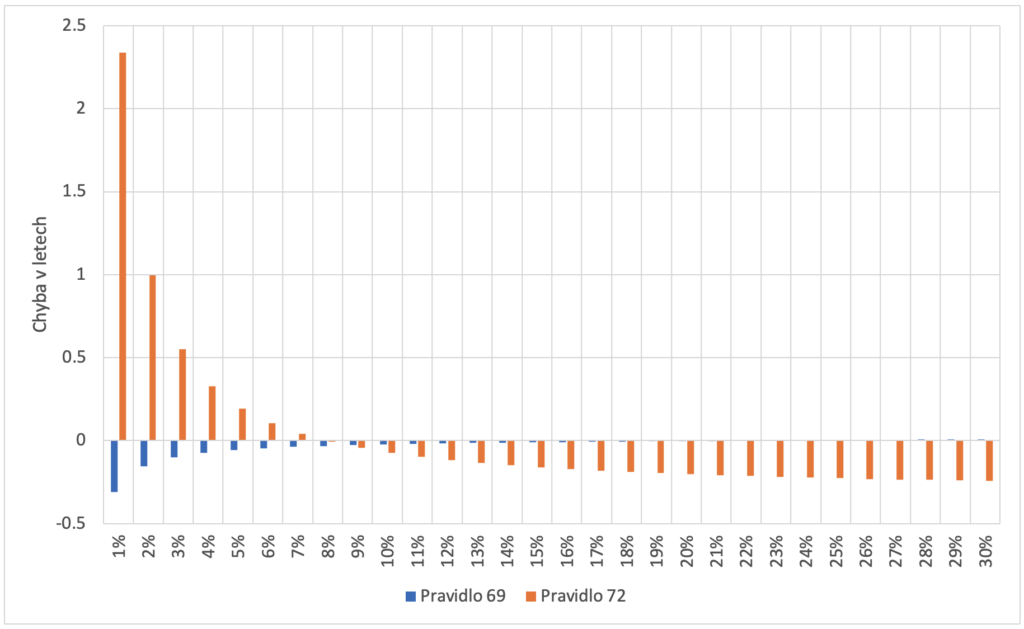
Zkusíme se podívat na chyby, kterých se dopouštíme při použití pravidel. Vezmeme úrokovou míru od 1 % až po 30 % a srovnáme výsledky aproximačních pravidel a přesného výpočtu. Jelikož na grafech průběhy poměrně dost splývají (což je dobře, tím je vidět, že aproximace funguje), tak ještě vyneseme chybu od přesného výpočtu. Zde vidíme, že pravidla 69 a 110 dosahují mnohem větší přesnosti.

Porovnání pravidel pro zdvojnásobení

Především na druhém grafu je patrné, že pravidlo 69 poskytuje mnohem přesnější výsledky.

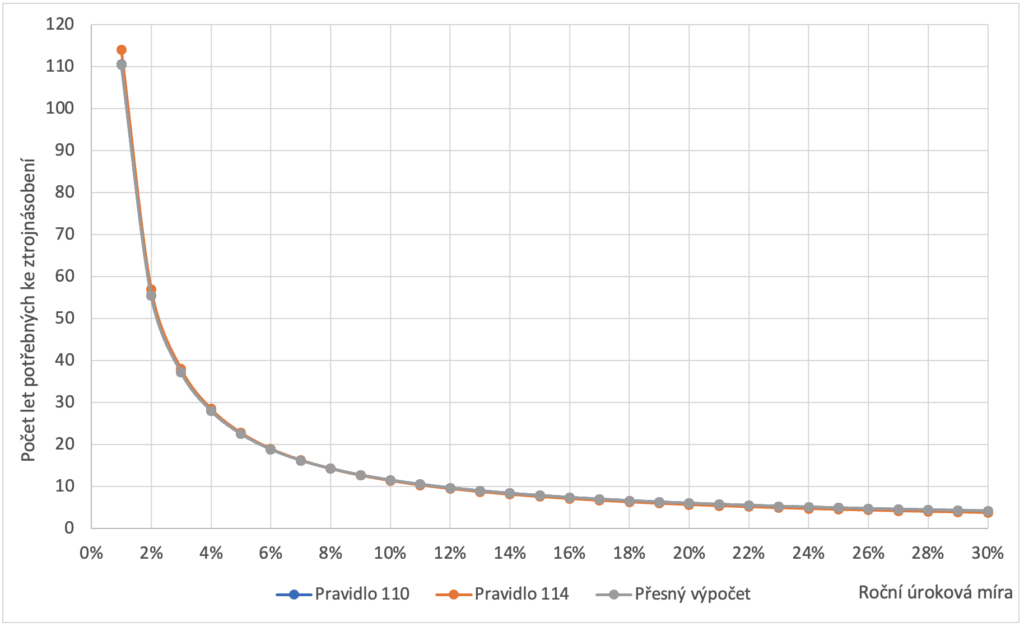
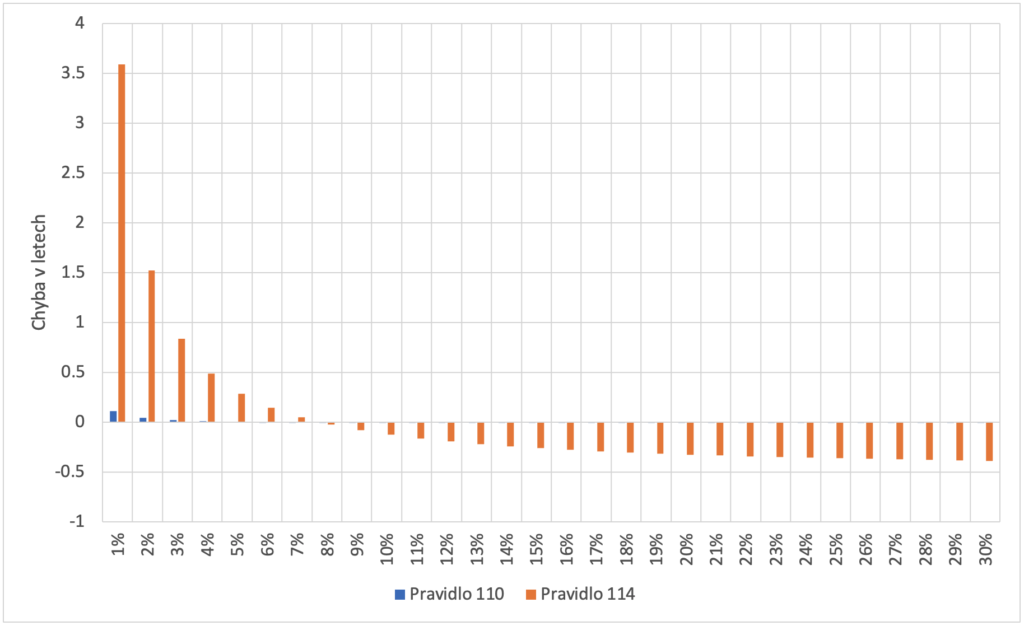
Počet let, které jsou potřebné pro zdvojnásobení vkladu dle všech tří metod výpočtu

Chyba, které se dopouštíme při použití obou aproximačních pravidel

Porovnání pravidel pro ztrojnásobení

Především na druhém grafu je patrné, že pravidlo 110 poskytuje mnohem přesnější výsledky.

Počet let, které jsou potřebné pro ztrojnásobení vkladu dle všech tří metod výpočtu

Pokud se Vám článek líbil, můžete nám přispět libovolnou částkou přes PayPal. Buď pomocí QR kódu (tím nás potěšíte víc, protože z poslaného nám dorazí vyšší částka, nebo pomocí tlačítka donate, kde dorazí trochu méně, než posíláte).

Prohlédněte si také naše služby: analýzy, výuka a doučování, tvorba a vyhodnocování dotazníků atd. na mStat – naše služby.

Tags:

aproximace finance počítání z hlavy pravidlo 110 pravidlo 114 pravidlo 69 pravidlo 72 složené úročení úrok

Categories:

Finanční matematika

Comments are closed

Statistické analýzy a poradenství